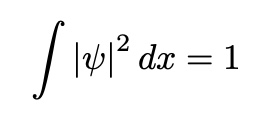First Order Differential Equation with one variable
- Euler’s Method
- Picard Method
- Predictor-Corrector Method
- Runge-Kutta Method ver.1: Second Order
- Runge-Kutta Method: General
- Second-Order Runge-Kutta Method
- Fourth-Order Runge-Kutta Method
Differential Equation with more than one variable
Second-Order Differencial Equations
Boundary Value problems
- shooting Method
- relaxation Method
- eigenvalue Problem
First-Order Differential Equations with One variable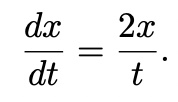
Ordinary Differential Equation(ODE)
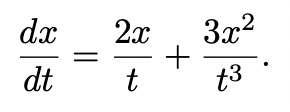non-linear can rarely be solved analytically
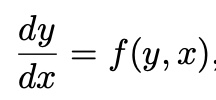computer don’t care whether a differential equation is linear or nonlinear
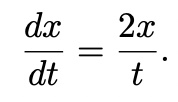Ordinary Differential Equation(ODE)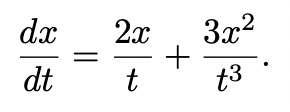non-linear can rarely be solved analyticallynon-linear ODE can be solved numerically
General form of a first-order one-variable ODE
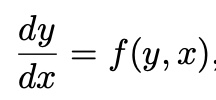computer don’t care whether a differential equation is linear or nonlineartechniques used for both cases are the same
- Euler's Method
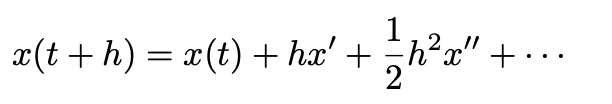
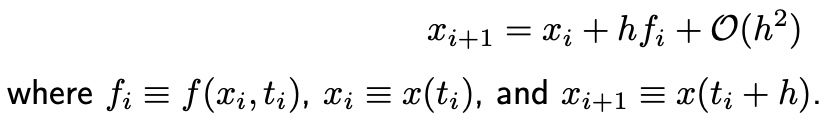
with Taylor expansion, f(x, t) around x:
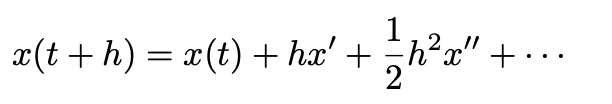
then,
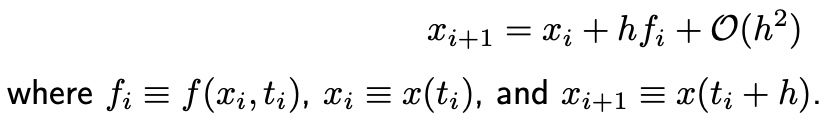
# dx/dt=-x^3+sin(t)
# initial state x=0 at t=0, t=[0, 10]
import numpy as np
import matplotlib.pyplot as plt
def f(x, t):
return -x**3+np.sin(t)
if __name__=="__main__":
t_i=0.; x_i=0
t_f=10.
N=1000
t=np.linspace(t_i, t_f, N)
x=np.zeros(len(t), float)
x[0]=x_i
h=t[1]-t[0]
for i in range(len(t)-1): # EM
x[i+1]=x[i]+f(x[i], t[i])*h
plt.plot(t, x)
plt.show()
- Picard Method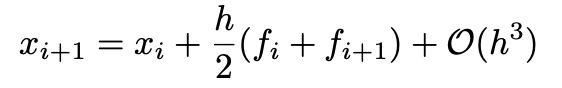
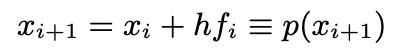(from Euler method)
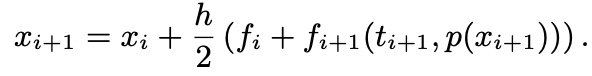
dx/dt=f(x, t) can be expressed as
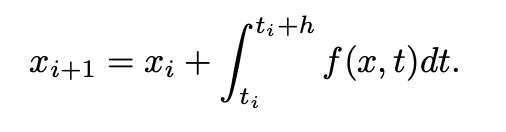
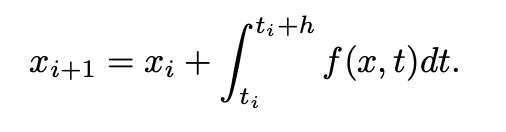
Use the trapezoidal method
일반적으로 f_i+1을 구하는데 x_i+1이 필요하다.
1) Apply as less accurate algorithm to predict the next value x_i+1(Predictor)
for example Euler's method
2) Apply a better algorithm to improve the new value(Corrector)
for example Picard method
- Predictor-Corrector Method(PCM)
calculate the predictor
(from Euler method)apply the correction by Picard method
# dx/dt= -x**3+sin(t)
import numpy as np
import matplotlib.pyplot as plt
def f(x, t):
return -x**3+np.sin(t)
t=np.linspace(0, 10, 1000)
pcx=np.zeros(len(t), float)
h=t[1]-t[0]
for i in range(len(t)-1): # PCM
px=pcx[i]+f(pcx[i], t[i])*h
pcx[i+1]=pcx[i]+h*(f(pcx[i], t[i])+f(px, t[i+1]))/2
plt.plot(t, pcx)
plt.show()
Predictor-Corrector Method(PCM)는 기존의 Euler method(EM)를 내부에서 한번 수행한 후,
추가적인 연산을 이용해 오차를 O(h^2)에서 O(h^3)으로 줄일 수 있다.
- Runge-Kutta Method: Second Order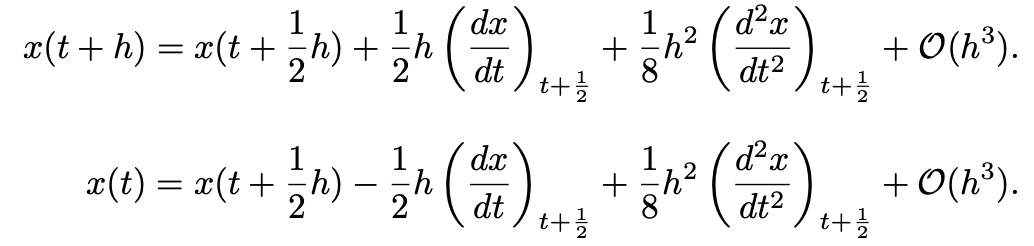
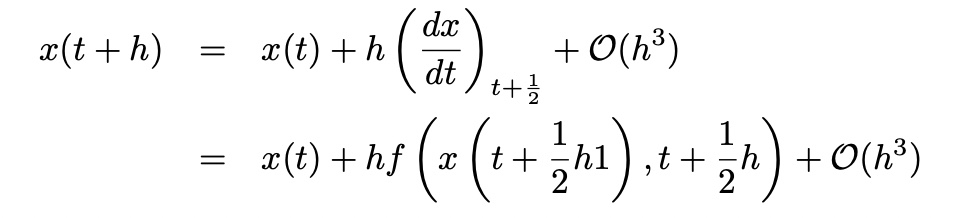
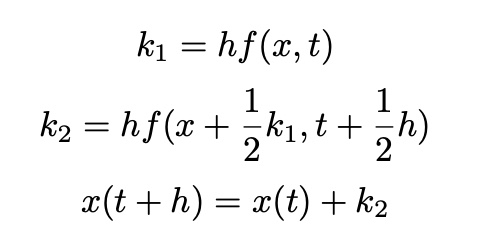
ver1)
Expansion x(t+h), x(t) around t+1/2h
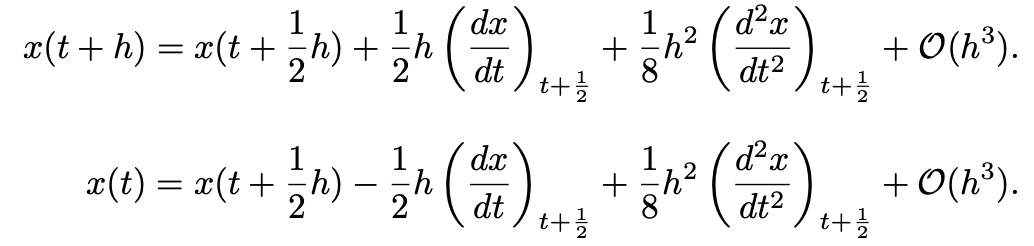
subtract,
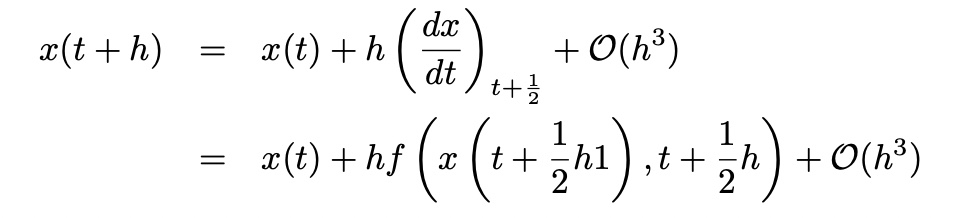
then,
Second-Order Runge-Kutta Method(RKM) ver1
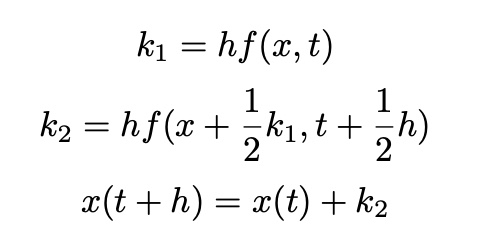
# Second-Order Runge-Kutta ver1
# dx/dt= -x**3+sin(t)
import numpy as np
import matplotlib.pyplot as plt
def f(x, t):
return -x**3+np.sin(t)
t=np.linspace(0, 10, 1000)
x=np.zeros(len(t), float)
x[0]=0
h=t[1]-t[0]
for i in range(len(t)-1): # RKM ver1
k_1=h*f(x[i], t[i])
k_2=h*f(x[i]+k_1/2, t[i]+h/2)
x[i+1]=x[i]+k_2
plt.plot(t, x)
plt.show()
Runge-Kutta Method: General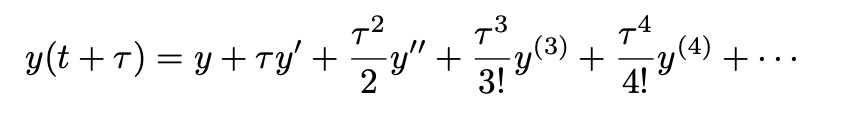
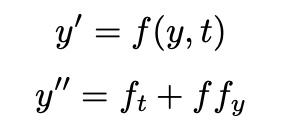
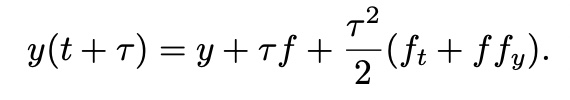
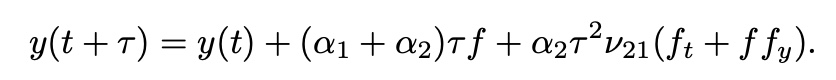
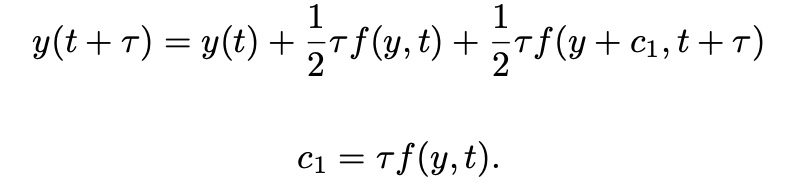
expand y(t+tau) at t with Taylor expansion
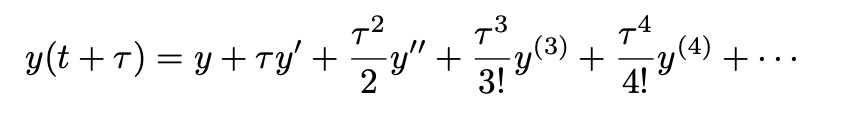
from solve
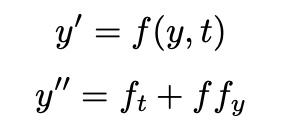
then, y(t+tau) also can be written as
O(tau^2) 항까지 고려 시,
::
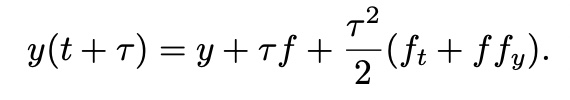
condition,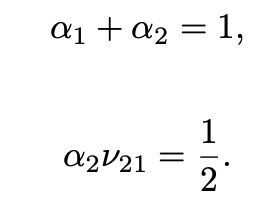 
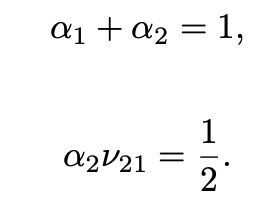
with choose alpha_1=1/2, alpha_2=1/2, mu_21=1
2nd-Order Runge-Kutta Method(RKM) ver2
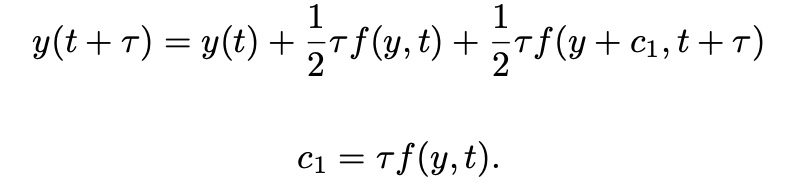
(2nd-order Runge-Kutta is the same with the Predictor-Corrector(or Modified Euler Method))
# Second-Order Runge-Kutta ver2
# dx/dt= -x**3+sin(t)
import numpy as np
import matplotlib.pyplot as plt
def f(x, t):
return -x**3+np.sin(t)
t=np.linspace(0, 10, 1000)
tau=t[1]-t[0]
alpha=[0.1, 0.2, 0.3, 0.4, 0.5]
for alpha_1 in alpha:
alpha_2=1-alpha_1; mu21=1/2/alpha_2
x=np.zeros(len(t), float)
x[0]=0
for i in range(len(t)-1): # RKM ver2
c_1=tau*f(x[i], t[i])
c_2=tau*f(x[i]+mu21*c_1, t[i]+mu21*tau)
x[i+1]=x[i]+alpha_1*c_1+alpha_2*c_2
plt.plot(t, x)
plt.show()
Fourth-Order Runge-Kutta Method
keep up to O(tau^4) we obtain the 4th-order RKM
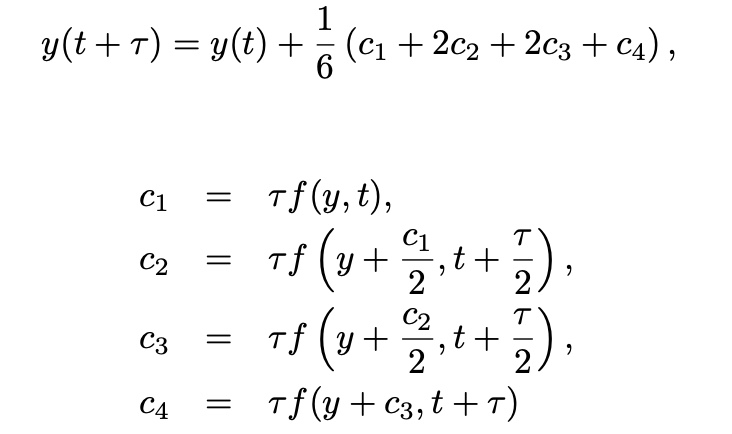가장 빈번하게 사용됨# Fourth-Order Runge-Kutta
# dx/dt= -x**3+sin(t)
import numpy as np
import matplotlib.pyplot as plt
def f(x, t):
return -x**3+np.sin(t)
t=np.linspace(0, 10, 1000)
x=np.zeros(len(t), float)
x[0]=0
tau=t[1]-t[0]
for i in range(len(t)-1): # 4-th order RKM
c_1=tau*f(x[i], t[i])
c_2=tau*f(x[i]+c_1/2, t[i]+tau/2)
c_3=tau*f(x[i]+c_2/2, t[i]+tau/2)
c_4=tau*f(x[i]+c_3, t[i]+tau)
x[i+1]=x[i]+(c_1+2*c_2+2*c_3+c_4)/6
plt.plot(t, x)
plt.show()
- The derivative of each variable can depend on
any of the variables
or all of the variables
the independent variable t as well
ex)
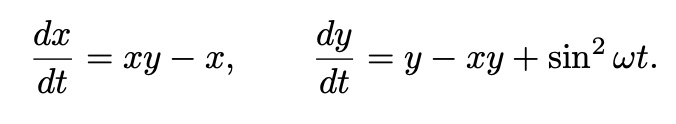
t만 independent variable
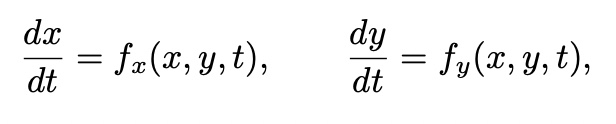
as
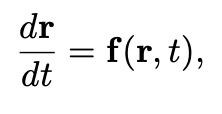
tend as ordinary differential equation, not partial differential equation
with Euler’s Method
with Fourth-Order Runge-Kutta Method
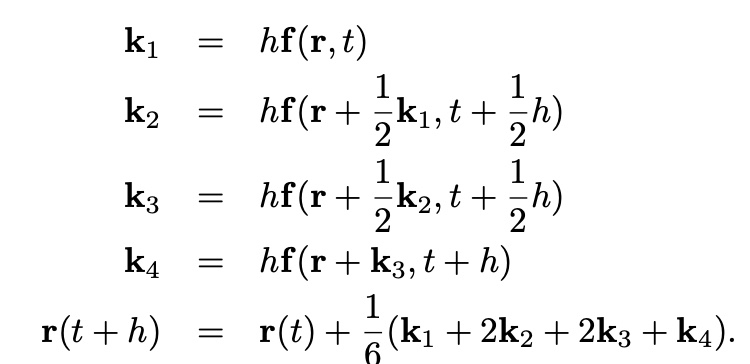(k, r is vector)# dx/dt=xy-x, dy/dt=y-xy+sin^2(wt)
# from t=0 to t=10 with w=1 and initial condition x=y=1 at t=0
import numpy as np
import matplotlib.pyplot as plt
def f(r, t): # dr/dt
x=r[0]
y=r[1]
fx=x*y-x
fy=y-x*y+np.sin(t)**2
return np.array([fx, fy], float)
if __name__=="__main__":
t=np.linspace(0, 10, 1000)
r=np.ones([len(t), 2])
#x=np.ones_like(t)
# y=np.ones_like(t)
k=np.zeros([4, 2], float) # Fourth Order Runge-Kutta Method
h=t[1]-t[0]
for i in range(1, len(t)): # Vector calculation
#r=[x[i-1], y[i-1]]
k[0]=h*f(r[i-1], t[i-1])
k[1]=h*f(r[i-1]+k[0]/2, t[i-1]+h/2)
k[2]=h*f(r[i-1]+k[1]/2, t[i-1]+h/2)
k[3]=h*f(r[i-1]+k[2], t[i-1]+h)
r[i]=r[i-1]+(k[0]+2*k[1]+2*k[2]+k[3])/6
plt.plot(t, r[:, 0])
plt.plot(t, r[:, 1])
plt.show()
Second-Order Differential Equations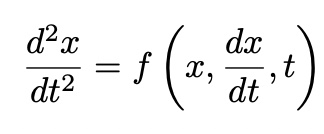
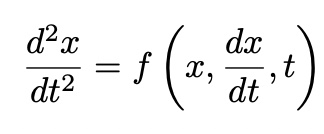
define a neew quantity
second-order ODE transform to two first-order ODEs
higher order ODEs also,
dx/dt를 새로운 변수 y로 선언해서, 기존의 두 변수에 대한 Runge-Kutta Method를 사용
# Nonlinear Pendulum
# m*L*d^2(theat)/dt^2=-m*g*sin(theta)
# equivalently d^2theta/dt^2=-g/L*sin(theat)
# set dtheta/dt=w
import numpy as np
import matplotlib.pyplot as plt
def f(r, t):
global g, L
f_theta=r[1]
f_w=-g/L*np.sin(r[0])
return np.array([f_theta, f_w])
t=np.linspace(0, 5, 1000)
h=t[1]-t[0]
theta=np.zeros(len(t))
omega=np.zeros(len(t))
# INITIAL STATE
theta[0]=np.pi-0.5*np.pi
omega[0]=0
g= 9.81; L=0.1
for i in range(len(t)-1): # 4-th order RKM
r=[theta[i], omega[i]]
k_1=h*f(r, t[i])
k_2=h*f(r+k_1/2, t[i]+h/2)
k_3=h*f(r+k_2/2, t[i]+h/2)
k_4=h*f(r+k_3, t[i]+h)
theta[i+1], omega[i+1]=r+(k_1+2*k_2+2*k_3+k_4)/6
plt.plot(t, theta)
plt.plot(t, omega)
plt.xlabel(r"$t$")
plt.ylabel(r"$\theta(t)$, $\omega(t)$")
plt.show()
Revisit Newton’s Equation of motion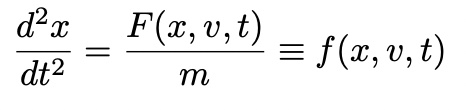
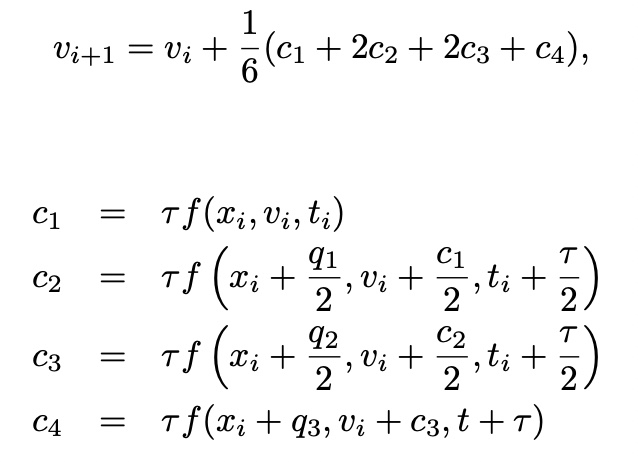
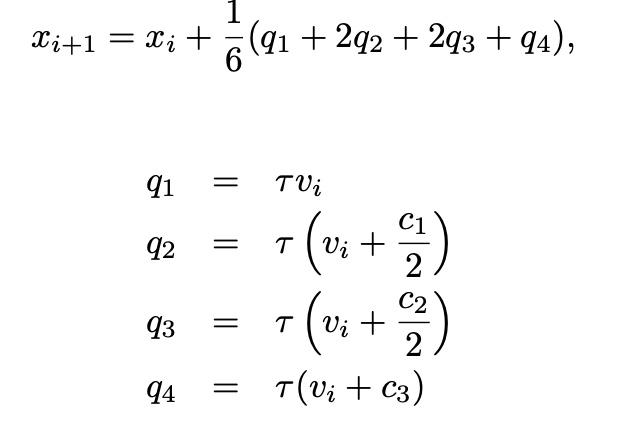
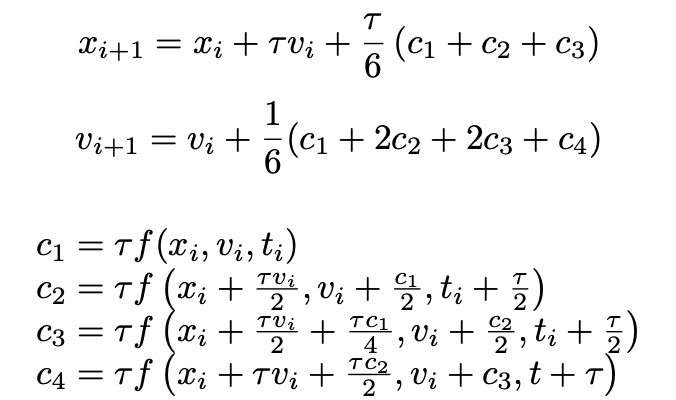
Newton’s method
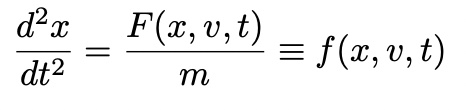
with 4th Runge-Kutta method
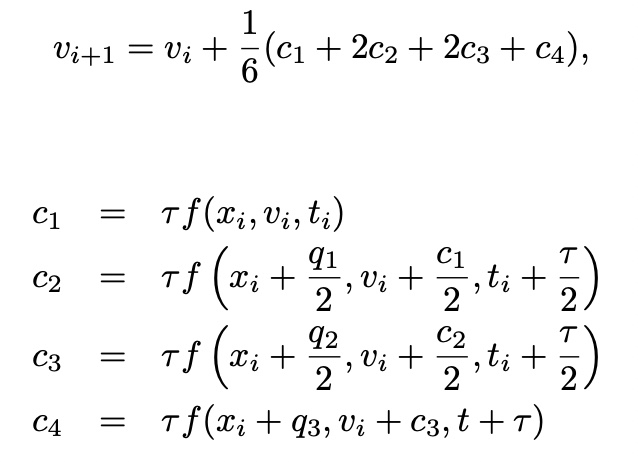
and
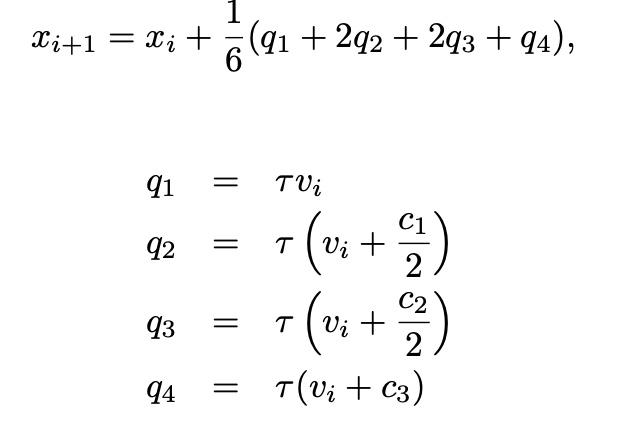
c, q가 independent 하지 아니한 경우 사용,
Revisit Newton’s Equation of motion
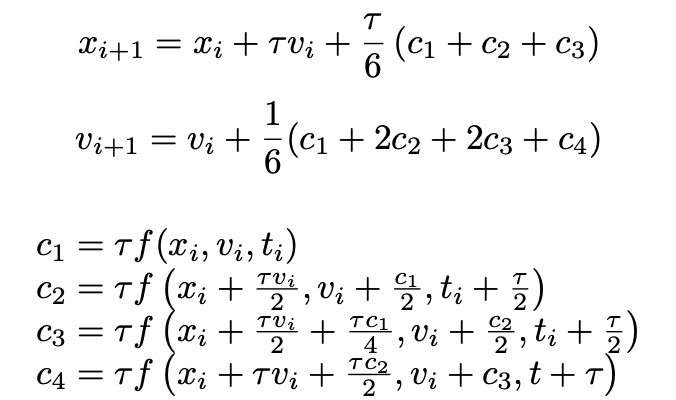
ex) Nonlinear Pendulum
# Revisit Method
# The Nonlinear Pendulum
# m*L*d^2(theat)/dt^2=-m*g*sin(theta)
import numpy as np
import matplotlib.pyplot as plt
def f(theta, omega, t):
global g, L
f_theta=omega
f_omega=-g/L*np.sin(theta)
return f_omega
t=np.linspace(0, 5, 1000)
h=t[1]-t[0]
theta=np.zeros(len(t))
omega=np.zeros(len(t))
# INITIAL STATE
theta[0]=np.pi-0.1*np.pi
omega[0]=0
g= 9.81; L=0.1
for i in range(len(t)-1): # 4-th order RKM
c_1=h*f(theta[i], omega[i], t[i])
c_2=h*f(theta[i]+h*omega[i]/2, omega[i]+c_1/2, t[i]+h/2)
c_3=h*f(theta[i]+h*omega[i]/2+h*c_1/4, omega[i]+c_2/2, t[i]+h/2)
c_4=h*f(theta[i]+h*omega[i]+h*c_2/2, omega[i]+c_3, t[i]+h)
omega[i+1]=omega[i]+(c_1+2*c_2+2*c_3+c_4)/6
theta[i+1]=theta[i]+h*omega[i]+h*(c_1+c_2+c_3)/6
plt.plot(t, theta, 'r-')
plt.plot(t, omega, 'b-')
plt.xlabel(r"$t$")
plt.ylabel(r"$\theta(t)$, $\omega(t)$")
plt.show()
ex) Van del Pol Oscillator
# d^x/dt^2=mu(x_0^2-x^2)dx/dt-w^2x
import numpy as np
import matplotlib.pyplot as plt
def f(x, v, t):
global x_0, mu, w
return mu*(x_0**2-x**2)*v-w**2*x
# RungeKutta
def RK4th(f, r, h, tmax):
x=[]; v=[]; t=[]
tt=0.
x.append(r[0]); v.append(r[1]); t.append(tt)
c=np.zeros(4, float)
i=0
while tt<=tmax: # 요부분이 가장 중요
c[0]=h*f(x[i], v[i], t[i])
c[1]=h*f(x[i]+h*v[i]/2, v[i]+c[0]/2, t[i]+h/2)
c[2]=h*f(x[i]+h*v[i]/2+h*c[0]/4, v[i]+c[1]/2, t[i]+h/2)
c[3]=h*f(x[i]+h*v[i]+h*c[1]/2, v[i]+c[2], t[i]+h)
xx=x[i]+h*v[i]+h*(c[0]+c[1]+c[2])/6
vv=v[i]+(c[0]+2*c[1]+2*c[2]+c[3])/6
x.append(xx)
v.append(vv)
tt+=h; i+=1
t.append(tt)
return x, v, t
if __name__=='__main__':
x_0=1; mu=1; w=1
r=[1, -5]
tmax=50
h=0.01
x, v, t=RK4th(f, r, h, tmax)
plt.plot(t, x)
plt.plot(t, v)
#plt.plot(x, v)
plt.show()
import matplotlib.animation as animation
ani=animation.FuncAnimation()
ani.save(“*.mp4”, fps=15)
를 이용해서 모션 그래프 생성 가능
Boundary Value Problems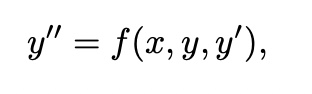
with second-order differential equation
four possible boundary condition sets:
- Shooting Method
- Relaxation Method
Shooting Method
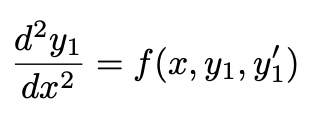
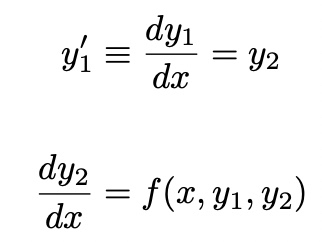
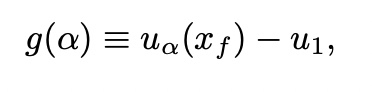find, g(alpha)=0 satisfied alpha
change the given boundary condition into the correspoding initial condition
through a trial-and-error method
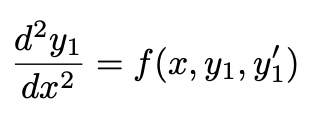
convert into two first-order differential equations:
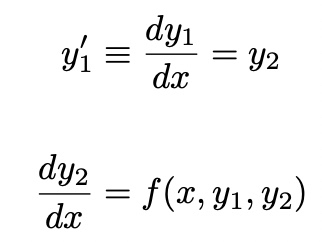
change the given boundary condition into the initial condition
with secant method(or bisection method)
adjust parameter alpha to satisfy y1(x_f)=u_1 (boundary condition)
find, g(alpha)=0 satisfied alphawith secant method(or bisection method)
해의 개수와 무관한 secant method를 사용하는 것이 좋음
# with bisection
# vertical position of a thrown ball
# d^2x/dt^2=-g
# b.c x=0 at time t=0 and t=10
# set dx/dt=v then dv/dt=-g
import numpy as np
import matplotlib.pyplot as plt
def f(r, t):
x=r[0]
v=r[1]
return np.array([v, -G], float)
def RK4(f, x, t, h):
c=np.zeros((4, 2), float)
c[0]=h*f(x, t)
c[1]=h*f(x+c[0]/2, t+h/2)
c[2]=h*f(x+c[1]/2, t+h/2)
c[3]=h*f(x+c[2], t+h)
return x+(c[0]+2*c[1]+2*c[2]+c[3])/6
def g(v, t):
r=np.array([0., v], float)
h=t[1]-t[0]
for i in range(len(t)-1):
r=RK4(f, r, t[i], h)
return r[0]-0.
if __name__=="__main__":
G=9.81
t_i=0.; t_f=10.
t=np.linspace(t_i, t_f, 1000)
# bisection
tolerance=1e-6
v1=0.001
v2=1000.
h1=g(v1, t)
h2=g(v2, t)
while abs(h2-h1)>tolerance:
vm=(v1+v2)/2
hm=g(vm, t)
if h1*hm>0:
v1=vm
h1=hm
else:
v2=vm
h2=hm
v_i=(v1+v2)/2
print("Needs Velocity: ", v_i, sep="")
x=np.zeros_like(t, float)
v=np.zeros_like(t, float)
v[0]=v_i
r=np.array([0, v_i], float)
h=t[1]-t[0]
for i in range(1, len(t)):
r=RK4(f, r, t[i-1], h)
x[i]=r[0]
v[i]=r[1]
plt.plot(t, x)
plt.show()
Secant method(순수한 Secant method는 아님)
# with secant
# vertical position of a thrown ball
# d^2x/dt^2=-g
# b.c x=0 at time t=0 and t=10
# set dx/dt=v then dv/dt=-g
import numpy as np
import matplotlib.pyplot as plt
def f(r, t):
x=r[0]
v=r[1]
return np.array([v, -G], float)
def RK4(f, x, t, h):
c=np.zeros((4, 2), float)
c[0]=h*f(x, t)
c[1]=h*f(x+c[0]/2, t+h/2)
c[2]=h*f(x+c[1]/2, t+h/2)
c[3]=h*f(x+c[2], t+h)
return x+(c[0]+2*c[1]+2*c[2]+c[3])/6
def g(v, t):
r=np.array([0., v], float)
h=t[1]-t[0]
for i in range(len(t)-1):
r=RK4(f, r, t[i], h)
return r[0]-0.
if __name__=="__main__":
G=9.81
t_i=0.; t_f=10.
t=np.linspace(t_i, t_f, 1000)
# secant
tolerance=1e-6
v1=0.001
v2=1.
h1=g(v1, t)
while abs(v2-v1)>tolerance:
h2=g(v2, t)
dv=v2-v1
dh=h2-h1
v1=v2
v2-=dv*h2/dh
h1=h2
print("Needs Velocity: ", v_i, sep="")
x=np.zeros_like(t, float)
v=np.zeros_like(t, float)
v[0]=v_i
r=np.array([0, v_i], float)
h=t[1]-t[0]
for i in range(1, len(t)):
r=RK4(f, r, t[i-1], h)
x[i]=r[0]
v[i]=r[1]
plt.plot(t, x)
plt.show()
Relaxation Method
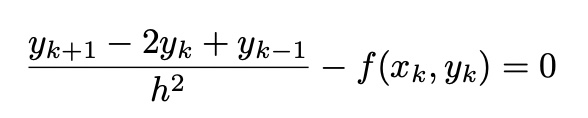
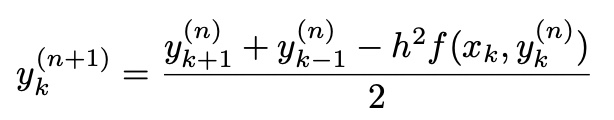
from Taylor expansion,
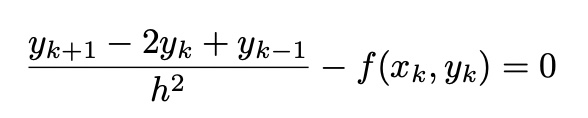
then,
Relaxation Method
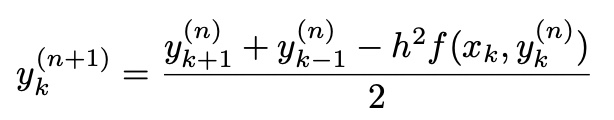
keeping the boundary condition, iteratively calculate y_k
Boundary Condition이 성립하도록 먼저 FIX 한 후, 미분 방정식 해 계산
# Relaxation Method
# vertical position of a thrown ball
# d^2x/dt^2=-g
# b.c x=0 at time t=0 and t=10
# set dx/dt=v then dv/dt=-g
import numpy as np
import matplotlib.pyplot as plt
def f(r, t):
global G
return -G
def RK4(f, x, t, h):
c=np.zeros((4, 2), float)
c[0]=h*f(x, t)
c[1]=h*f(x+c[0]/2, t+h/2)
c[2]=h*f(x+c[1]/2, t+h/2)
c[3]=h*f(x+c[2], t+h)
return x+(c[0]+2*c[1]+2*c[2]+c[3])/6
if __name__=="__main__":
G=9.81
t_i=0.; t_f=10.
t=np.linspace(t_i, t_f, 100)
h=t[1]-t[0]
x=np.zeros_like(t, float)
x[0]=x[-1]=0.
x_tmp=np.zeros_like(x, float)
delta=1.
tolerance=1e-5
n=0
while delta>tolerance:
n+=1
for k in range(1, len(t)-1): # boundary k=0, k=len(t)-1 포함 X
x_tmp[k]=(x[k+1]+x[k-1]-h**2*f(x[k], t[k]))/2
delta=max(abs(x-x_tmp))
x, x_tmp=x_tmp, x
print("TRY: ", n, sep="")
plt.plot(t, x)
plt.show()
-Schodinger Equation
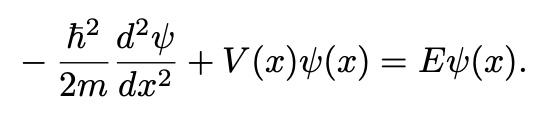Time-Independent Shrodinger Equation
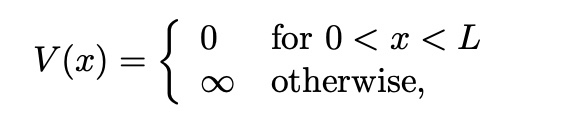
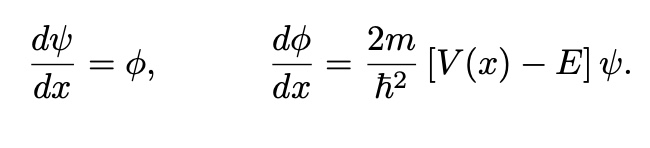
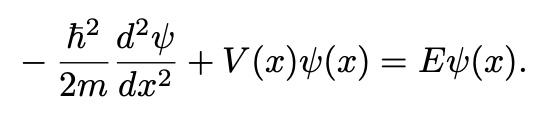Time-Independent Shrodinger Equationwith Infinite Square potential
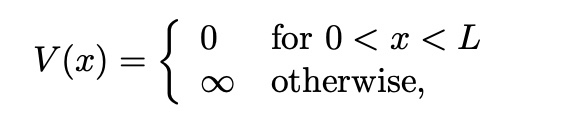
then Boundary condition
to Solve TISE
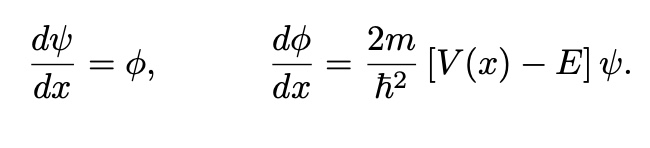
in order to solve problem,
Change the Energy E
